Sistema de Equações

Sistema Equações

Algebra: Regra de três

Regra de três é calculo meio dificil se resolver presta bem atenção:

Como podem ver ele usando em fração sobre 100 ou qualquer numero ,mais outra quando problema é para diminui você deverá inverter fração para antes de fazer regra de três.
Por que chama de regra de três? Neste calculo você usa somente 3 cálculos diferente por isso tem este nome.  

álgebra: Equação de primeiro grau

álgebra é o ramo que estuda as generalizações dos conceitos e operações de aritmética. Hoje em dia o termo é bastante abrangente e pode se referir a várias áreas da matemática.

resumo são tipo cálculos com letras:

Expressão numéricas com sinais de - ou +

As Expressões numéricas que levar sinais + ou - são bastante diferente.
Ex:
(+8)+(-3)+(+7)=
+8-3+7 =
+5+7 = 12 

(-7)+(-3)+(-7) = 
- 7 +3 + 7=
 -4+7 =
= 3  

OBS: Quando tem numero com mesmo sinal é soma
e Quando for diferente deverá fazer uma conta de subtrair.
 

Conjunto Z

Desvendando o Mundo Oculto dos Números Inteiros: Além do Zero!

Olá, exploradores da matemática! Se você pensa que os números se resumem àqueles que usamos para contar as maçãs na feira, prepare-se para uma viagem surpreendente ao universo dos números inteiros, um conjunto numérico muito mais vasto e cheio de nuances do que você imagina!

veja reta numérica 

Esqueça o Básico: Uma Nova Dimensão Numérica!

Nós já conhecemos os números naturais (aqueles bonitinhos: 1, 2, 3...). Eles são ótimos para contar coisas positivas, mas e quando precisamos representar o que está "abaixo de zero" ou o que "falta"? É aí que entram em cena os números inteiros, representados pela elegante letra Z (uma homenagem à palavra alemã para "números", "Zahlen").

A Reta Numérica: Seu Mapa para o Mundo dos Inteiros!

Imagine uma estrada infinita que se estende para os dois lados. No meio dessa estrada, temos um ponto crucial: o zero (0). Essa é a nossa linha divisória no mundo dos números inteiros!

• Para a direita do zero: Aqui encontramos os velhos conhecidos, os números inteiros positivos (+1, +2, +3...). Eles são como os números naturais, mas com um sinal de "+" (que muitas vezes nem precisa aparecer, de tão amigos que já somos deles!).

• Para a esquerda do zero: E aqui está a grande novidade! Uma terra misteriosa de números menores que zero: os números inteiros negativos (-1, -2, -3...). Eles não indicam "nada", mas sim uma quantidade que está faltando, uma dívida, uma temperatura congelante ou uma posição à esquerda do nosso ponto de partida.

• O Zero: O Ponto de Equilíbrio: O zero é o mestre dessa reta numérica, o ponto de equilíbrio perfeito. Ele não é nem positivo nem negativo, mas sim o divisor de águas entre esses dois mundos numéricos.

(Imagine aqui uma imagem mental da reta numérica com o zero no centro, positivos à direita e negativos à esquerda)

Além da Reta: Onde os Inteiros Brilham na Vida Real!

Pensar nos números inteiros apenas na reta numérica é como admirar um carro parado. A verdadeira emoção está em ver onde eles nos levam! Os números inteiros são ferramentas poderosas em diversas situações do nosso dia a dia:

• Seu Bolso: Um saldo positivo na conta bancária é um número inteiro positivo. Uma dívida no cartão de crédito? Um número inteiro negativo! O zero representa aquela conta zerada (raridade, hein?).
• O Termômetro: 25°C é um inteiro positivo (que bom!), mas -5°C nos lembra daquele frio de gelar a alma (um inteiro negativo!). O 0°C é aquele ponto de transição, onde a água pode virar gelo ou líquido.
• Mapas e Localização: Se você está no térreo de um prédio, pode ser o andar 0. Subir é ir para os inteiros positivos (1°, 2°, etc.), e descer ao estacionamento ou subsolo nos leva aos inteiros negativos (-1, -2, etc.).
• A História no Tempo: O ano 50 d.C. é um inteiro positivo. Mas e os eventos "antes de Cristo"? Usamos números inteiros negativos para representá-los (ex: -50, que seria 50 a.C.).
• Jogos e Competições: Ganhar pontos é somar inteiros positivos, perder pontos é subtrair (adicionar inteiros negativos!).

Conclusão: O Universo Completo dos Números!

O conjunto dos números inteiros nos oferece uma visão muito mais completa do mundo numérico. Ele não se limita ao que podemos contar diretamente, mas também nos permite quantificar a ausência, a falta e as posições relativas. Da simples contagem de objetos à representação de conceitos abstratos, os números inteiros são uma ferramenta fundamental para entendermos o mundo ao nosso redor.

Então, da próxima vez que você vir um sinal de menos, lembre-se: você está entrando no fascinante mundo dos números inteiros, um universo que vai muito além do zero!

Gostou de expandir seus horizontes numéricos? Compartilhe essa descoberta com seus amigos e continue explorando as maravilhas da matemática conosco!

Numeiros decimais

 Numeros decimais são incompletos ( não possuem parte inteira)








Parte decimal é dividida em 
Primeira Base Décimos
Segunda Base Centésimos 
Terceira  base  Milésimos


Como nos podemos fazer para ler um simples numeiro decimal:

35,5 = Trinta e cincos inteiros e cino decimos 

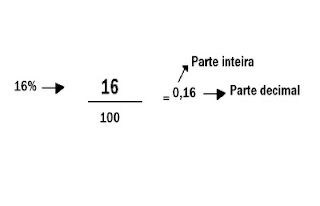
Desvendando a Porcentagem: Um Guia Simples e Prático

Olá pessoal! Hoje vamos mergulhar em um conceito matemático que faz parte do nosso dia a dia: a porcentagem. Seja para calcular um desconto naquela roupa que você tanto quer, entender o aumento do preço da gasolina ou analisar dados estatísticos, a porcentagem está sempre presente. Mas, afinal, o que ela significa e como podemos calculá-la de forma fácil?

O Que Significa Porcentagem?

A palavra "porcentagem" vem do latim "per centum", que traduzimos como "por cento". O símbolo que usamos para representá-la é o famoso "%". Pense nele como uma forma abreviada de dizer "de cada cem".

Imagine uma pizza dividida em 100 pedaços iguais. Se alguém come 18 desses pedaços, dizemos que essa pessoa comeu 18% (dezoito por cento) da pizza. Isso significa que, de um total de 100 partes, 18 foram consumidas.

A Porcentagem como Fração

Essa ideia da pizza nos leva a um ponto crucial: uma porcentagem nada mais é do que uma fração com denominador 100.

• Exemplo:
  • 18% é o mesmo que a fração 10018​.
  • 50% é equivalente a 10050​ (que simplificando, é 21​).
  • 100% representa 100100​, ou seja, o todo (1 inteiro).

Calculando a Porcentagem de um Número: Passo a Passo Simples

Agora, vamos ao que interessa: como calcular a porcentagem de um determinado valor? Vamos usar o exemplo que você trouxe: quanto é 18% de 300?

Existem duas formas principais (e equivalentes) de fazer esse cálculo:

Método 1: Usando a Fração

1. Transforme a porcentagem em fração: O primeiro passo é escrever a porcentagem como uma fração com denominador 100. No nosso exemplo, 18% se torna 10018​.

2. Multiplique o número pela fração: Agora, multiplicamos o número do qual queremos encontrar a porcentagem (que é 300) por essa fração:

   $$ 300 \times \frac{18}{100} $$

3. Realize a multiplicação: Multiplicamos o número pelo numerador da fração:

   $$ \frac{300 \times 18}{100} = \frac{5400}{100} $$

4. Divida pelo denominador: Por fim, dividimos o resultado pelo denominador (que é 100):

   $$ \frac{5400}{100} = 54 $$

   Portanto, 18% de 300 é 54.

Método 2: Usando o Decimal

Outra maneira de pensar é transformar a porcentagem em um número decimal antes de multiplicar:

1. Converta a porcentagem em decimal: Para fazer isso, basta dividir a porcentagem por 100. No nosso exemplo, $18\%÷100=0,18$.

2. Multiplique o número pelo decimal: Agora, multiplicamos o número original pelo valor decimal obtido:

   $$ 300 \times 0,18 = 54 $$

   Novamente, chegamos ao mesmo resultado: 18% de 300 é 54.

Conclusão:

Calcular porcentagens pode parecer complicado à primeira vista, mas a verdade é que se resume a trabalhar com frações (com denominador 100) ou números decimais. Entendendo que a porcentagem representa uma parte de um todo dividido em 100 partes, o processo de cálculo se torna muito mais intuitivo.

Esperamos que esta explicação tenha desmistificado a porcentagem para você! Use esses métodos simples no seu dia a dia e veja como esse conceito matemático se torna muito mais acessível.

Fique ligado para mais dicas e explicações matemáticas no nosso blog!