A lógica matemática analisa determinada proposição buscando identificar se representa uma afirmação verdadeira ou falsa.
A princípio, a lógica era ligada à filosofia, tendo sido iniciada por Aristóteles (384-322 a.C.) que se baseava na teoria do silogismo, ou seja, em argumentações válidas.
A lógica só passou a ser uma área da Matemática a partir dos trabalhos de George Boole (1815-1864) e Augustus de Morgan (1806-1871), quando eles apresentaram os fundamentos da lógica algébrica.
Essa mudança de paradigma tornou a lógica matemática uma importante ferramenta para a programação de computadores.
Proposições
As proposições são palavras ou símbolos que expressam um pensamento com um sentido completo e indicam afirmações de fatos ou de ideias.
Essas afirmações assumem valores lógicos que podem ser verdadeiros ou falsos e para representar uma proposição usualmente utilizamos as letras p e q.
São exemplos as proposições:
- O Brasil está localizado na América do Sul. (proposição verdadeira).
- A Terra é um dos planetas do sistema solar. (proposição verdadeira).
.(proposição verdadeira).
- A Terra é plana. (proposição falsa).
. (proposição falsa)
Considerando a lógica matemática, uma proposição não pode ser ao mesmo tempo verdadeira e falsa. Além disso, não existe a possibilidade de uma terceira situação diferente de verdadeiro ou falso.
As proposições podem ser simples, quando apresentam apenas uma sentença, e compostas quando são formadas pela combinação de duas ou mais proposições simples.
"O céu é azul" é um exemplo de proposição simples, já a sentença "O céu é azul e as nuvens são brancas" é um exemplo de proposição composta.
Conectivos
As proposições simples que formam uma proposição composta são ligadas por elementos que são chamados de conectivos. Além disso, também podemos utilizar conectivos para modificar uma proposição.
Na proposição "O céu é azul e as nuvens são brancas" o elemento e é um conectivo que une duas proposições, já na proposição "O céu não é azul" o conectivo não modifica a proposição.
Tabela Verdade
Quando temos proposições compostas, os valores lógicos resultantes dependem única e exclusivamente dos valores de cada proposição simples.
Diante disso, utilizamos um dispositivo chamado tabela verdade ou tabela de verdade, onde são colocados os valores de cada proposição e de acordo com os conectivos presentes chegamos ao valor lógico final.
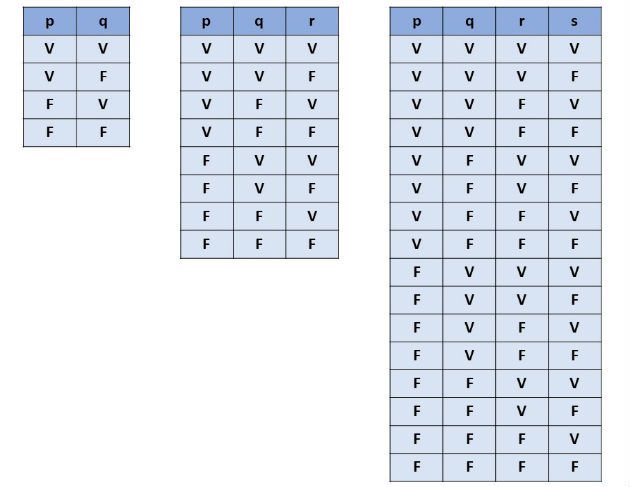
Em uma tabela verdade, o número de linhas e de colunas dependerá da quantidade de proposições simples que formam a proposição composta, sendo que em cada coluna é colocada uma proposição.
Abaixo apresentamos a tabela verdade para duas, três e quatro proposições:
Operações Lógicas
As operações feitas a partir de proposições são chamadas de operações lógicas. Este tipo de operação segue as regras do chamado cálculo proposicional.
As operações lógicas fundamentais são: negação, conjunção, disjunção, condicional e bicondicional.
Negação
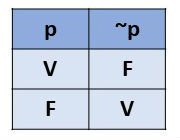
Esta operação representa o valor lógico oposto de uma dada proposição. Desta forma, quando uma proposição é verdadeira, a não proposição será falsa.
Com o objetivo de indicar a negação de uma proposição colocamos o símbolo ~ na frente da letra que representa a proposição, assim, ~p significa a negação de p.
Exemplo
p: Minha filha estuda muito.
~p: Minha filha não estuda muito.
~p: Minha filha não estuda muito.
Como o valor lógico da não proposição é o inverso da proposição, teremos a seguinte tabela verdade:
Conjunção
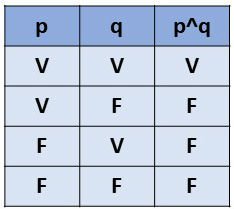
A conjunção é utilizada quando entre as proposições existe o conectivo e. Esta operação será verdadeira quando todas as proposições forem verdadeiras.
O símbolo utilizado para representar essa operação é o ^, colocado entre as proposições. Desta forma, quando temos p ^ q, significa "p e q".
Desta forma, a tabela verdade desse operador lógico será:
Exemplo:
Sendo p: 3 + 4 = 7 e q: 2 + 12 = 10 qual o valor lógico de p ^ q?
Solução
A primeira proposição é verdadeira, mas a segunda é falsa. Portanto, o valor lógico de p e q será falso, pois esse operador só será verdadeiro quando ambas as sentenças forem verdadeiras.
Disjunção
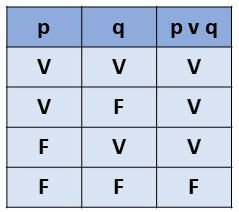
Nesta operação, o resultado será verdadeiro quando pelo menos uma das proposições é verdadeira. Sendo assim, será falso apenas quando todas as proposições forem falsas.
A disjunção é usada quando entre as proposições existe o conectivo ou e para representar esta operação é usado o símbolo v entre as proposições, assim, p v q significa "p ou q".
Levando em consideração que se uma das proposições for verdadeira o resultado será verdadeiro, temos a seguinte tabela verdade:
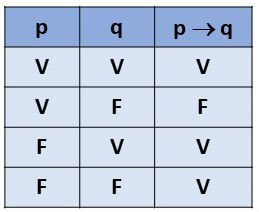
Condicional
A condicional é a operação realizada quando na proposição utiliza-se o conectivo se... então.... Para representar esse operador usamos o símbolo →. Assim, p → q significa "se p, então q".
O resultado desta operação só será falso quando a primeira proposição for verdadeira e a consequente for falsa.
É importante ressaltar que uma operação condicional não significa que uma proposição é a consequência da outra, o que estamos tratando é apenas de relações entre valores lógicos.
Exemplo
Qual o resultado da proposição "Se um dia tem 20 horas, então um ano tem 365 dias"?
Solução
Sabemos que um dia não tem 20 horas, logo essa proposição é falsa, também sabemos que um ano tem 365 dias, logo essa proposição é verdadeira.
Desta forma, o resultado será verdadeiro, pois o operador condicional só será falso quando a primeira for verdadeira e a segunda falsa, que não é o caso.
A tabela verdade para esse operador será:
Bicondicional
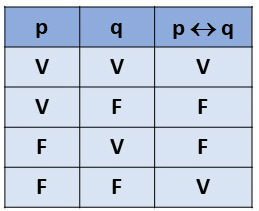
O operador bicondicional é representado pelo símbolo  e indica uma proposição do tipo ...se e somente se.... Portanto,
e indica uma proposição do tipo ...se e somente se.... Portanto,  significa "p se e somente se q", ou seja, p é condição necessária e suficiente para q.
significa "p se e somente se q", ou seja, p é condição necessária e suficiente para q.
Ao usar esse operador, a sentença será verdadeira quando as proposições forem ambas verdadeiras ou ambas falsas.
Os possíveis resultados que podemos encontrar ao usar esse operador estão na tabela abaixo:
Exemplo
Qual o resultado da proposição "30 = 2 se somente se 2 + 5 = 3"?
Solução
A primeira igualdade é falsa, pois 30 = 1 e a segunda também é falsa (2 + 5 = 7), desta maneira, como ambas são falsas, então, o valor lógico da proposição é verdadeiro.
Nenhum comentário:
Postar um comentário